After a lot of reading on wikipedia

I finally came up with this equation.
If you have an acceleration over a certain amount of time, starting at a certain velocity, it will calculate the distance travelled in that time-step.
Code:
do
input "Enter start velocity:",start_velocity#
input "Enter acceleration:",acceleration#
i = 1
while i <= 16
nums = 16/i
dist# = 0.0
vel# = start_velocity#
for n = 1 to nums
inc dist#,Integrate(vel#,acceleration#,i)
inc vel#,acceleration#*i
next n
print "Over "+str$(nums)+" steps of duration " + str$(i) + ", total distance travelled is " + str$(dist#)
i = i*2
endwhile
wait key
loop
function Integrate(start_velocity#, acceleration#, time_step#)
move# = (time_step#*time_step#*acceleration#+2.0*start_velocity#*time_step#)/2.0
endfunction move#
This example program shows that however long each time-step is, as long as the total time is the same it will always return the same distance travelled.
Normally, people use this equation:
distance# = velocity#*time_step#
velocity# = acceleration#*time_step#
However, surprisingly that will give different results with a higher or lower frame-rate! This is because it only approximates the velocity/time graph.
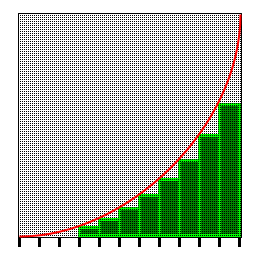
In a velocity/time graph, the area under the line is the distance travelled.
This graph shows how the area is calculated in the normal equation:
And for the same equation on a slower computer:
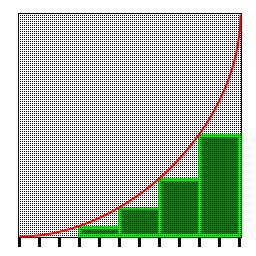
The green area is what is added up to get the distance, and it is different on different speeds of computer.
My equation calculates it exactly for the whole area under the curve, and so does not change with the frame-rate!
