Sorry your browser is not supported!

Ok, I've been scratching my head over this problem for a while. Since I know a lot of people here like a challenge that stirs the grey matter, I thought I'd throw it out to you guys for your thoughts.

I have a bunch of objects arranged on a grid, represented here as green square. Overlapping this green squares are red circles which can touch one or more green squares.

The challenge:
Define a set of lists which contain the numbers of the red circles with the following rules:
1. All circles must be accounted for
2. No more than 5 circles per list
3. Get the minimum number of lists
4. If a green square is touched by more than 1 circle those circles must appear in the same list
5. A circle may appear in more than 1 list

Here's a graphical reference:


The second line by itself is an easy example. One possible solution is:
[1,2,3,4]
[4,5,6,7]
1. All circles are accounted for
2. There are no more than 5 circles per list
3. This is the minimum number of lists, as 1 list is impossible with 7 circles
4. Circle 4 appears in both lists so that there is no list which contains a circle which touches a green box without containing the other circle which also touches that box.

For reference, you can consider the boxes also have an ID (they are identified in the program, so can be interrogated for which circles touch them and stored/remembered. As you can see the problem is fairly straight forward to work out visually, but turning it into psuedo-code is another matter.

All help appreciated! I'll continue working on it and post any findings I came up with.

Here's pseudo so far for the easy example:

1. For every box, create a list of touching circles:
[1] [1,2] [2,3] [3,4] [4,5] [5,6] [6,7] [7]

2. Remove duplicates (there aren't any, but it's a good step to include anyway).

3. Remove lists which are sub-lists, so [1] is a sub-list of [1,2], and [7] is a sub-list of [6,7]
[1,2] [2,3] [3,4] [4,5] [5,6] [6,7]

4. Group first list with a list containing as many same circle numbers as possible ensuring the circle count stays under 5.
[1,2] + [2,3] = [1,2,3]
[1,2,3] [3,4] [4,5] [5,6] [6,7]

5. Repeat until max 5 count is reached:
[1,2,3] + [3,4] = [1,2,3,4]
[1,2,3,4] [4,5] [5,6] [6,7]
[1,2,3,4] + [4,5] = [1,2,3,4,5]
[1,2,3,4,5] [5,6] [6,7]

6. Group is now full, so move onto next group and repeat:
[5,6] + [6,7] = [5,6,7]
[1,2,3,4,5] [5,6,7]

That works for the simple group, but whether it works for the larger group is hard to test. I'll do a diagram somewhere between the two and then do the same working .....

Ok, here goes!



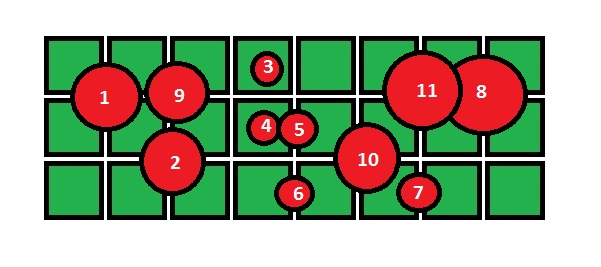
1. For every box, create a list of touching circles:
[1] [1,9] [9] [3] [] [11] [8,11] [8]
[1] [1,2,9] [2,9] [4,5] [5,10] [10,11] [8,11] [8]
[] [2] [2] [6] [6,10] [7,10] [7] []

2. Remove duplicates (and empty lists!):
[1] [1,9] [9] [3] [] [11] [8,11] [8]
[1] [1,2,9] [2,9] [4,5] [5,10] [10,11] [8,11] [8]
[] [2] [2] [6] [6,10] [7,10] [7] [][/b]

[1] [1,9] [9] [3] [11] [8,11] [8] [1,2,9] [2,9] [4,5] [5,10] [10,11] [2] [6] [6,10] [7,10] [7]

3. Remove lists which are sub-lists:
[3] [8,11] [1,2,9] [4,5] [5,10] [10,11] [6,10] [7,10]

4. Group first list with a list containing as many same circle numbers as possible ensuring the circle count stays under 5. Repeat until max 5 count is reached:
[3] + [8,11] = [3,8,11] (nothing else contains 3!)
[3,8,11] [1,2,9] [4,5] [5,10] [10,11] [6,10] [7,10]
[3,8,11] + [10,11] = [3,8,10,11] (most matching numbers)
[3,8,10,11] [1,2,9] [4,5] [5,10] [6,10] [7,10]
[3,8,10,11] + [5,10] = [3,5,8,10,11] Group full!
[3,5,8,10,11] [1,2,9] [4,5] [6,10] [7,10]

6. Group is now full, so move onto next group and repeat:
[1,2,9] + [4,5] = [1,2,4,5,9] No groups with matching numbers. Full!
[3,5,8,10,11] [1,2,4,5,9] [6,10] [7,10]

Next group:
[6,10] + [7,10] = [6,7,10]
[3,5,8,10,11] [1,2,4,5,9] [6,7,10]

Done!

And it looks like this. So it looks like I may have solved my own problem!



The final requirement and test is that each square can be assigned one list. On assigning it to that list, every circle that touches that square should be in that list. Looking at the graphic that looks like it's true.

So basically what I think I've done is created a thread with lots of odd looking graphics, masses of working text which means nothing to anybody, and solved my own problem.

Thanks for your time and I owe you all a drink.

Here's an algorithm which may be equivalent to yours.

The first part works like a flood-fill algorithm. Each flood fill produces a new group of circles.

1. Each circle starts off unassigned to a group
2. Repeat 3-7 until all circles have been assigned a group:
3. Create a new group
4. Create a set of circles to be processed, and add any unassigned circle
5. Repeat 6-7 until the set of circles to be processed is empty
6. Pick any circle in the set and remove it, then add it to the current group
7. For each square under that circle, add any other unassigned circles touching that square to the set (assuming they are not already in it)

Now all the circles have been divided into groups. For each group of size N>5, divide it into a group of 5 and a group of N-4 until there are no groups larger than 5. (This part could be combined with the previous stage)

Now use a greedy algorithm to combine groups together up to a maximum of 5.

Hah. Cheers for that Diggsey. Sounds like it could work in theory. I'll have a go with it on paper as I did with the other and see how it works out. If it's less complex to code it's a winner. CPU strain isn't an issue to ease of coding takes priority. I shall report back tomorrow.

If the squares have a specific size and the circles have a defined radius then it shouldn't be hard to tick off the squares that the circles cover. When a new circle is being placed, first check if the squares it covers have already been ticked off, if so then try another position. Repeat until all circles have been placed or until the 're-try' count has been exhausted.

EDIT: It's actually very similar to a piece I was working on last week placing planets and moons on a grid for my game project. I had to check the distance between previously successful placements and grid coordinates.

I don't see the reason for duplicating circles in different lists.